kencomアプリで楽しみながら、健康に。
あなたに合わせた健康情報をお届けして、
楽しく健康になる毎日を提供します。
登録済みの方
あなたの健康状態に合わせた健康情報をお届けします
あなたの健康状態を分析し、
おすすめの健康ニュースを配信します。
現役医師のコラム、管理栄養士のレシピ、
クスッと笑えて役立つ
健康のトリビアなど
盛りだくさん。
Aさんの記事
- 血圧の高い人向け減塩のコツ
- 動脈硬化を防ぐ方法
- お腹に効く筋トレ
Bさんの記事
- 貧血予防の食事
- 冷え性対策
- 運動不足解消法
- 血圧
- 脂質
- 運動不足
- 貧血
- 冷え性
- 運動不足
年に1回の健診結果を忘れないように
あなたの健診結果をkencomアプリで
簡単に確認できます。
リスクの高い疾患がわかったり、
健康状態の
過去の変化がグラフで一目で確認できます。
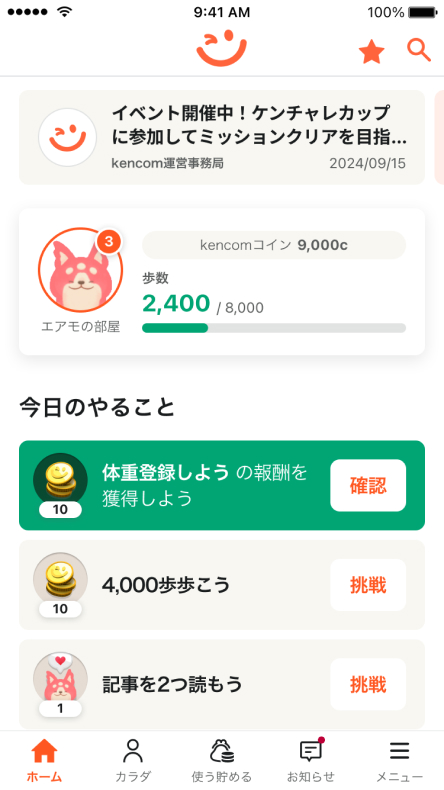
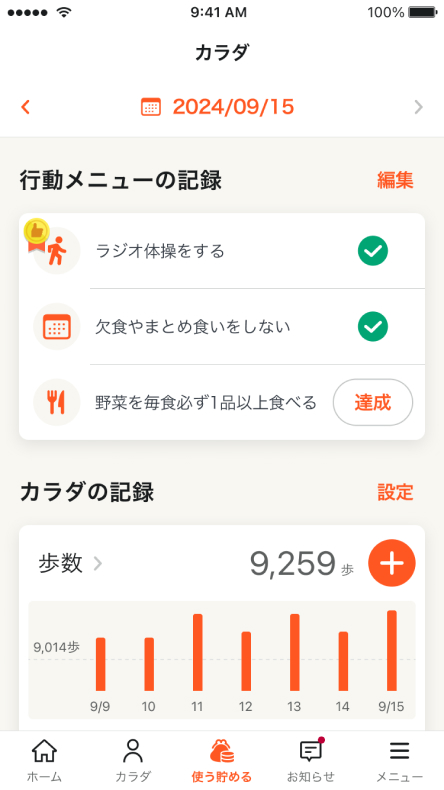
今日歩いた歩数をアプリが教えてくれる
今日はたくさん歩いたな〜と思った時はアプリを開いて
みてください。kencomアプリが自動で歩数を取得して、
どれだけ歩いたかグラフで見せてくれますよ。
コインを貯めて、ギフト券を当てよう!
毎日kencomを使うたびに
kencomコインがもらえます。
貯まったコインを使って、ギフト券が
当たるゲームで運試しはいかが?
まずは3日間試してみましょう
アプリをダウンロードしてkencomを使う
Apple および Apple ロゴは米国その他の国で登録された Apple Inc. の商標です。App Store は Apple Inc. のサービスマークです。
Google Play および Google Play ロゴは Google LLC の商標です。
kencom アプリ (Android 版) のプライバシーポリシーはこちら (https://kencom.jp/android_privacy_policy) からご覧頂けます。
2次元コードを読み取ってアプリをダウンロード
QR